Ev Ware - Evolutionary Simulation

Introduction
Leon Brillouin, an early pioneer of information theory, writes [1]
The [computing] machine does not create any new information, but it performs a very valuable transformation of known information.
A supporting statement made more recently by Christensen and Oppacher [2], is that conservation of information (e.g.. the no free lunch theorem) in computer simulation, especially in evolutionary computing [3, 4, 5], is
... very useful, especially in light of some of the sometimes-outrageous claims that had been made of specific optimization algorithms
An example is the computer program dubbed ev [6]. Using evolutionary programming with a reference to DNA, ev purports to:
- show "how life gains information." Specifically "that biological information... can rapidly appear in genetic control systems subjected to replication, mutation and selection."
- illustrate punctuated equilibrium: "The transition [i.e. convergence] is rapid, demonstrating that information gain can occur by punctuated equilibrium."
- disprove "Behe’s [7] definition of ‘irreducible complexity’ ... ('a single system composed of several well-matched, interacting parts that contribute to the basic function, wherein the removal of any one of the parts causes the system to effectively cease functioning'.) "
These claims are contrary to Brillouin's initial insight. The Ev Ware Simulation shows Brillouin to be correct. Indeed, the claims of ev exemplify seductive semantics characteristic in some areas of computational intelligence [8] wherein results of computer programs "are interpreted too literally, resulting in meanings being inferred that are more profound and important than warranted." [9].
We begin with a high level description of ev and the Ev Ware Simulation. A more detailed analysis corroborating the performance of the simulation is available [10].

Random Search for the Output Target
I flip a coin 130 times and record each outcome as a one for heads and zero for tails. I now have 130 bits (zeros and ones) and ask you to guess them. When you give me your 130 bits, I compare them to mine and respond "yes" or "no" as to whether they match. You are doing a random undirected search. The probability of you randomly identifying the specific sequence is one chance out of
1,361,100,000,000,000,000,000,000,000,000,000,000,000.
On the Ev Ware Simulation you can search for a string of ones and zeros using a random undirected search. To simulate flipping a coin 130 times, choose Random Binding Sites on the Target Type menu.

Each simulation chooses a different set of coin flips. On the pull down Algorithm menu, choose Undirected Search: Random Output.

Click on Start Search (Auto):

The search then begins. You will see rows of ones and zeros that look like this.

The grey and white row of ones and zeros on the bottom is the target. These are coin flips you are trying to guess and, as the search continues, they remain the same. The top blue and white row of ones and zeros is your guess of the target. In essence, to make a guess in Undirected Search: Random Output, you flip a coin 130 times to generates 130 bits and ask if your string of ones and zeros is identical to the target. If so, the search has been completed successfully. If not, you try again with 130 more coin flips. The blue and white row of ones and zeros continually changes as we try to find the target.
But don't wait for the Ev Ware Simulation to give you the right answer. If you made one trillion guesses per second (and the simulation is far from this fast!) it would take you, on average, 12,566,000,000,000,000,000 (twelve and a half quintillion) years to find the target. This assumes you never ask the same question twice.
This is why ev looks so spectacular. The ev evolutionary search algorithm finds such a target against what looks like miniscule odds! This looks like creation of a lot of information by evolutionary programming. As we will show, this is far from being the case.

The Digital Organism
To find a specified target, the ev search uses a chain of A,C,G,D nucleotides found in DNA. Since there are four possible nucleotides in each position, each is assigned a number (in base 2 or as a location index) as A = 0, C = 1, G = 2, and T = 3. Some of these numbers are used as input values. Others are used as parameters in what we will call a number cruncher. Here is an illustration.
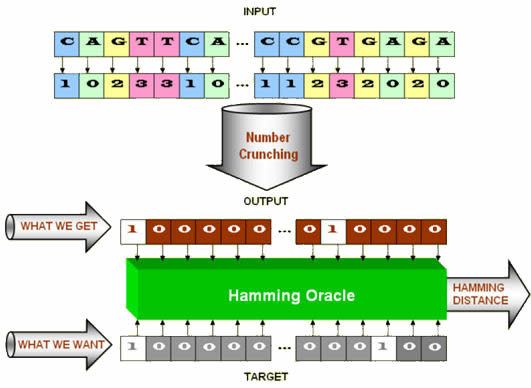 Figure 1. The structure of a digital organism in ev.
Figure 1. The structure of a digital organism in ev.
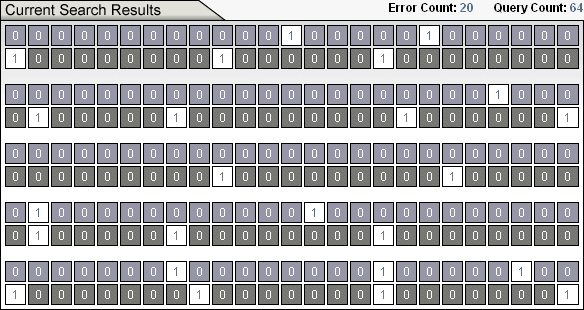
The number cruncher takes the input, crunches it, and spits out a sequence of ones and zeros. Ones correspond to binding site location and zeros to a non-binding site. The digital organism contains a Hamming oracle that compares the computed output (what we get) to the desired target (what we want) and tells us how many of the bit pairs do not match. This difference is dubbed the Hamming distance. For example, the Hamming distance between the string 000 111 011 and 001 110 101, is 4. (An example Hamming error from the Ev Ware Simulation is discussed in Sidebar 1.) All of this constitutes the digital organism pictured in Figure 1.
In evolution models, there is survival of the fittest. For the digital organism, the lower the Hamming distance, the better the fitness. The smaller the Hamming distance, the closer the output is to the target. Using the structure of the digital organism in Figure 1, our job is to find the target as quickly and efficiently as possible.
The Rules
The rules of our game are simple. We pretend we do not know what the target is. We only know the Hamming distance (or as it is referred to on the simulation interface, the Error Count.) Using only this information, our job is to construct an output that matches the target. The game is won when the Hamming distance is zero and the output and the target are the same.
The ability of ev to find its target in much less that twelve and a half quintillion years is not due the evolutionary program. It is, rather, the active information [3] residing in the structure of the ev digital organism that allows one to find string of nucleotides that gives an output that matches the target. Active information can be defined as any structure or procedure that aids in finding the target. For the ev structure shown in Figure 1, there are two major sources of active information: the Hamming oracle and the structure of the number cruncher.
The search rules allow us to use any part of the original ev structure to find the unknown target. We are allowed to change any nucleotide in the digital organism including the input and nucleotides that effect the number cruncher. Like ev, we can also use the Hamming oracle. We can also choose to not use part of the available ev structure.
There are many strategies to search for the target using the same tools used by ev. Some are better than others. The better procedures, much better than the evolutionary search used by ev, illustrate the enormous active information provided by digital organism structure - especially the Hamming oracle.
We will show that the ability of ev to find its target is not due to the evolutionary algorithm used, but is rather due to the active information residing in the digital organism. This active information was provided by the designer of the computer software.

Targets
There are many targets of ones and zeros we can use. The ev program uses the sparse pattern of ones in a sea of zeros shown in gray and white in Sidebar 1. We can alternately choose a target of all zeros, or we can choose the target randomly using simulated coin flipping. Here is what the target choices looks like in the Ev Ware Simulation.


Undirected Search Using Random Inputs
Instead of the output string of ones and zeros, we can randomly choose the input set of nucleotides that generate the input and the parameters for the number cruncher in Figure 1. To do a random search this way, choose Undirected Search: Random Input from the pull down menu. It looks like this.

Random nucleotides (A,C,G,T) are chosen for each query. We can think of the choice of an A, G, C, or T as a sequence of two coin flips. (Recall that A = 0, C = 1, G = 2, and T =3. We can write this in binary as A = 00, C = 01, G = 10 and T = 11.)
The number cruncher spits out a corresponding sequence of ones and zeros. We use the Hamming oracle and announce either
- NO. The output string does not match the target. Try again, or
- YES! The output string matches the target.
Here is an undirected search that powerfully illustrates that the input and number cruncher in evfavors some outputs over others. Choose, as a target, all zeros as shown here.

Randomly choosing nucleotides typically generates all zeros in only a few hundred tries! In general, the digital organism is designed to generate output bit streams of mostly zeros and a few ones, or mostly ones with a few zeros. (If you are interested in why, the math is here.) Note that the target used by ev is mostly zeros with a few ones. (See the sequence of gray and white bits in Sidebar 1.) Finding the ev binding sites using randomly chosen sequences of nucleotides still takes a long time, but far shorter than twelve and a half quintillion years.
The structure of the digital organism therefore contributes to generating outputs that are close to the target used by ev. It is a source of active information.

The Hamming Oracle
Biological evolution oft claims to be non-teleological, meaning there is no target. Since the digital organism has a target, this is not the case for ev. By generating the Hamming distance between the output and the target, the Hamming oracle is telling us whether we are getting closer or further from the target. An analogy is an Easter egg hunt where a single egg is hidden in 50 acres of forest. Finding that Easter egg with no information about its location is difficult. If, however, someone analogous to the Hamming oracle tells the egg seeker they are getting closer to the egg (a smaller Hamming distance means "You're getting warmer!") or further from the egg (a larger Hamming distance means "You're getting colder!"), then finding the egg becomes much easier.

Using the Hamming Oracle to Find the Target: Five Search Techniques
An enormous amount of active information can generally be extracted from a Hamming oracle. The target sequence is found much more quickly than with no active information.
 There are many ways to use the Hamming oracle. We describe those simulated by the Ev Ware Simulation. Some are more successful than others thereby illustrating there are good and bad ways to extract information from an oracle. The evolutionary ev program, it turns out, is far from the best way of using the Hamming oracle.
There are many ways to use the Hamming oracle. We describe those simulated by the Ev Ware Simulation. Some are more successful than others thereby illustrating there are good and bad ways to extract information from an oracle. The evolutionary ev program, it turns out, is far from the best way of using the Hamming oracle.
We have already discussed two examples of underutilizing the Hamming oracle. Both Undirected Search: Random Output and Undirected Search: Random Input use it as a needle in a haystack oracle. We care only if the Hamming distance is zero:
"We found a solution!!"
or not
"This isn't it. Try again."
1. Undirected Search: Random Output. If we choose all of the output bits at random, the chance of generating the target using repeated independent trials at the output is near zero. We can choose random bit streams for centuries and not get the right answer.

2. Undirected Search: Random Input. We can alternately choose random nucleotides (A,C,G,T) to establish the input and the parameters for the number cruncher. If the generated output string of bits matches the target, we claim success. Otherwise, we randomly choose another set of random nucleotides and try again.

The Hamming oracle gives us the Hamming distance between the output and the target. Thus far we have made use only whether the Hamming distance is zero or not. In other words, we have used it only as a needle in a haystack oracle. That's not an efficient use of this Hamming oracle. We can use it more efficiently to extract even more active information per query thereby reducing the difficulty of the search further.
3. Ratchet Search. Ratchet search, an example of an evolutionary strategy, is an available search option on the Ev Ware Simulation. It makes use of the numerical value of the Hamming distance (or, as called in the simulation, the Error Count) as opposed to the needle in a haystack oracle which only cares if the Hamming distance is zero or not.
 Ratchet Search initially chooses at random a single set of nucleotides that, in turn, determine the input and the number cruncher parameters of the digital organism. Then one nucleotide is chosen at random and, with equal chance, replaced with an A, C, G, or T. There is 1 chance in 4 the nucleotide won't change because the new randomly selected nucleotide is identical to the nucleotide being replaced. A different nucleotide will either change the input or a parameter in the number cruncher. The result is that there will probably be a different output bit stream. The Hamming distance measure of the error is computed for both the old and new outputs. If the Hamming distance resulting from the new nucleotide sequence is smaller or equal to the old, the nucleotide replacement is kept. If the Hamming distance is larger, we are getting "colder." The nucleotide change is then rejected and we revert back to the old nucleotide and choose another nucleotide to change. This process is repeated if the target has not yet been found.
Ratchet Search initially chooses at random a single set of nucleotides that, in turn, determine the input and the number cruncher parameters of the digital organism. Then one nucleotide is chosen at random and, with equal chance, replaced with an A, C, G, or T. There is 1 chance in 4 the nucleotide won't change because the new randomly selected nucleotide is identical to the nucleotide being replaced. A different nucleotide will either change the input or a parameter in the number cruncher. The result is that there will probably be a different output bit stream. The Hamming distance measure of the error is computed for both the old and new outputs. If the Hamming distance resulting from the new nucleotide sequence is smaller or equal to the old, the nucleotide replacement is kept. If the Hamming distance is larger, we are getting "colder." The nucleotide change is then rejected and we revert back to the old nucleotide and choose another nucleotide to change. This process is repeated if the target has not yet been found.
It is now clear why we call this Ratchet Search. Once a smaller Hamming distance is achieved, it is ratcheted into place and is guaranteed to never get bigger. This is not the same as being assured the search will converge exactly to the target.
To use Ratchet Search, simply choose Ratchet Search on the Algorithm pull down menu.

4. Hamming Search. Hamming Search reveals the enormous information available from the Hamming oracle. Like Undirected Search: Random Output, the Hamming Search looks directly at the output string of bits and totally disregards any nucleotides, input or number cruncher. There is no use of a digital organism. The search is directly performed at the output and its repeated comparison with the target. Add one to the number of bits in the target and that's the maximum number of queries needed to identify the target. If there are 130 bits in the target, it takes only 131 queries to to find out what these bits are! This illustrates the enormous information available from the Hamming oracle.

Here's how the Hamming search works. Choose at random an output set of bits and find the Hamming distance between it and the target. Next, choose the first bit and "flip" it, i.e., if it is a zero, make it a one and if it is a one make it a zero. Present the modified output to the Hamming oracle. If the Hamming distance gets larger, the original bit was right. If the Hamming distance decreases, we leave the bit flipped. Either way, we are assured that the first bit in the output is now correct. The process is repeated for the second bit, and so on. If there are N bits, it takes N + 1 queries to the Hamming oracle to identify all of the bits in the target. And, as discussed in one paper, we can do even better!
The Hamming Search reveals the enormous active information available from the Hamming oracle.
5. Ev Search. The Ev Search Algorithm is the search algorithm used in the original ev paper [6]. So far, we have only dealt with one digital organism. For Ev Search, we start with 64 digital organisms. Each has as its target the ev binding sites so the Target Type box should look like this.

Each digital organism has different randomly chosen nucleotides assigned to it. Using these nucleotides, the input and number cruncher are created and the output string of bits is generated. Each digital organism then evaluates the Hamming distance (Error Count) for its nucleotides. The half of the population with the worst (biggest) Hamming distance is killed off and the half with the best (smallest) Hamming distance are not only kept, but duplicated to take the place of the newly deceased digital organisms. The population count is thus restored to 64 organisms. By killing the weak and duplicating the strong, we have simulated survival of the fittest.
Next comes mutation. A different single nucleotide is randomly chosen in each of the digital organisms. It is replaced by a randomly selected A, G, C, or T nucleotide. (Like Undirected Search: Random Input, there is a one in four chance the new nucleotide is the same as the old one.) All of the 64 organisms have been mutated. The fitness of the new organisms is then determined by evaluating the Hamming distances, and the process of survival of the fittest and mutation is repeated. Each cycle of survival of the fittest and mutation is a generation. Success is achieved when the Hamming distance of any of the 64 organisms reaches zero. In the single implementation reported, ev identified the target in 704 generations [6] or about 45 thousand queries.

With the Ev Ware Simulation you can choose the number of digital organisms you want. The default, as shown immediately above, is ev's use of 64. You can also choose the number of nucleotides mutated every generation. The ev program uses one mutation. The percent survival can also be chosen. The ev program lets 50% survive.

Query Counting
During computation, the Ev Ware Simulation displays Error Count and Query Count.

The Error Count is the Hamming distance between the output and target as displayed. For Ev Search, the display is of the digital organism with the lowest error in the population.
Why are we interested in the Query Count? In evolutionary computing, the computation of fitness typically dominates computer time. Thus, tallying of queries is a good way to compare the performance of different searches. For Undirected Search: Random Input, Ratchet Search, and Ev Search, a query requires placing the input through the number cruncher and evaluating the Hamming distance of the output to the target. Undirected Search: Random Output (the poorest of the five searches used by the Ev Ware Simulation) and Hamming Search (the best) do not use inputs nor the number cruncher. The only component of the digital organism that is used is the Hamming oracle. A query in these two searches is therefore much less costly in computer time than the others.

The Ev Ware Simulation Interface
The Ev Ware Simulation has identical modules on the top and bottom that allow choice of any combination of two searches using any two targets. The two searches will run simultaneously allowing real time observation of performance and seeing which search is winning the race. Here is a screen capture example.
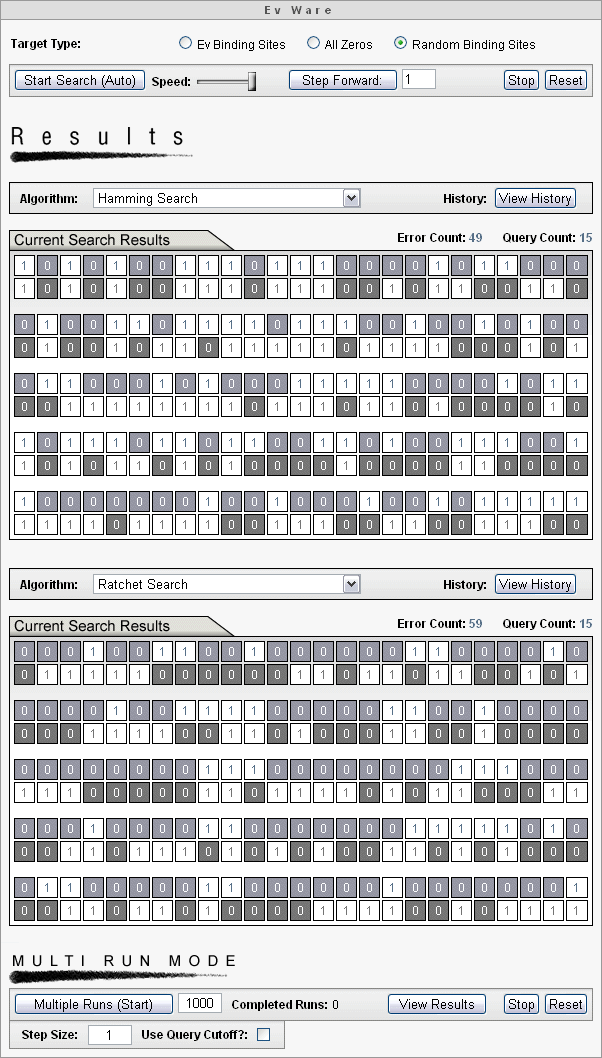
When a search is complete, the iteration for that simulation stops. When both searches have been completed successfully, the simulation interface displays the following.


Final Remarks
From our dissection of the ev digital organism, claims about the computer program can now be made.
- ev purports to show "how life gains information." Specifically "that biological information... can rapidly appear in genetic control systems subjected to replication, mutation and selection." It is the active information introduced by the computer programmer and not the evolutionary program that reduced the difficulty of the problem to a manageable level.
- ev purports to show illustrate punctuated equilibrium: "The transition [i.e. convergence] is rapid, demonstrating that information gain can occur by punctuated equilibrium." The active information from the Hamming oracle and ev's number cruncher are responsible for the rapid convergence - not the evolutionary program.
- ev purports to disprove "Behe's [7] definition of ‘irreducible complexity’ ... ('a single system composed of several well-matched, interacting parts that contribute to the basic function, wherein the removal of any one of the parts causes the system to effectively cease functioning'.)" Billions of input nucleotide sequences will produce the binding sites required by ev.
Lastly, we note that all of the active information available from the ev organism has not been used. Thus far, the Hamming oracle's output has only been used as (a) a needle in a haystack oracle or (2) as a method to determine whether one solution is better than another. We have not used the exact numerical value provided by the Hamming oracle. Efficient use of this information to reduce the number of queries remains open. One such search technique where a 130 bit target can be successfully identified in significantly less than 130 queries has been identified [10].

Source Code
The source code for the Ev Ware Simulation is available for download, as a zip file.
Our Ev Ware implementation does not claim exact duplication of the original software. Inverse software engineering inevitably leads to differences. The Ev Ware Simulation, for example, does not preserve on ties, it simply keeps the top N organism according to the selection scheme.
Ev Ware Simulation implementation by Atom.

References
- [1] Leon Brillouin, Science and Information Theory (Academic Press, New York, 1956). Second Edition, Dover (2004).
- [2] S. Christensen and F. Oppacher, “What can we learn from No Free Lunch? A First Attempt to Characterize the Concept of a Searchable,” Proceedings of the Genetic and Evolutionary Computation (2001).
- [3] William A. Dembski and Robert J. Marks II “Conservation of Information in Search: Measuring the Cost of Success” IEEE Transactions on Systems, Man and Cybernetics A, Systems & Humans, vol.5, #5, September 2009, pp.1051-1061 [ link ]
- [4] William A. Dembski, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (Lanham, Md.: Rowman and Littlefield, 2002).
- [5] David Wolpert and William G. Macready, “No free lunch theorems for optimization”, IEEE Trans. Evolutionary Computation 1(1): 67-82 (1997).
- [6] T.D. Schneider, “Evolution of Biological Information,” Nucleic Acids Research, Vol. 28, No 14, pp.2794-2799 (2000) [ pdf | html ] - Last Accessed 03/12/2010)
- [7] Michael J. Behe, Darwin's Black Box: The Biochemical Challenge to Evolution, Free Press, 2nd edition (2006).
- [8] J.C. Bezdek, “What is computational intelligence?” in Computational Intelligence: Imitating Life, 1994 - Institute of Electrical & Electronics Engineers (IEEE), edited by J.M. Zurada, R.J. Marks II and C.J. Robinson
- [9] Russell C. Eberhart and Yuhui Shi, Computational Intelligence: Concepts to Implementations, (Morgan Kaufmann, 2007)
- [10] William A. Dembski & Robert J. Marks II, “Judicious Use of Computational Resources in Evolutionary Search”
Ev Ware History
- December 28, 2008: Version 3.0 released
- February 14, 2009: Version 3.1 released
- March 12, 2010: Version 3.2 released