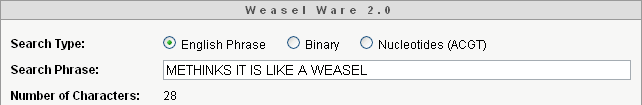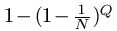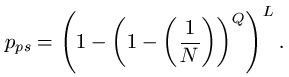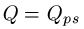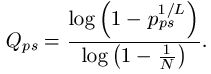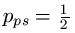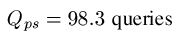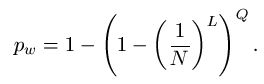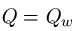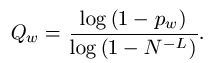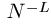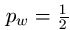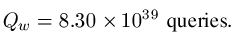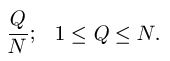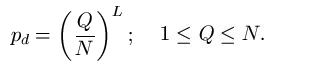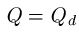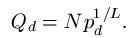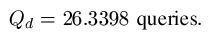Weasel Ware - Evolutionary Simulation
Introduction
Unassisted search will not work for even moderately sized problems [1, 2]. Monkeys at a typewriter eventually generating the complete works of Shakespeare is simply impossible. Simple combinatorics show the universe as modeled by science today is not sufficiently old nor big enough to support the search for even a hand full of pages [3, 4]. Neither are the 101000 parallel universes hypothesized by M-theory [1].
Rather than illustrating the evolutionary reproduction of all of the works of Shakespeare, Professor Richard Dawkins opted for a single phrase from Shakespeare's Hamlet [5].
METHINKS*IT*IS*LIKE*A*WEASEL
The phrase has L = 28 letters from an alphabet of N = 27 characters: 26 letters and a space. The space is shown here with an asterisk.
After admission that random search will not work, Dr. Dawkins proposes an algorithm rich in active information that guides the search to a quick success. In evolutionary computing, active information must be imposed on the search algorithm to allow even moderately sized search algorithms to work. In evolutionary computing, as in Dr. Dawkins' example, active information is supplied by the programmer. The principle of conservation of information requires it [2].

From Whence the WEASEL Cometh?
To illustrate evolution, Dawkins starts with the phrase [5]

New phrases 'breed from' this random phase. "It duplicates it repeatedly, but with a certain chance of random error - 'mutation' - in the copying." Every 10th was recorded and the results were [5]

The target phrase,
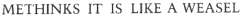
was reached in 64 generations.
Without a detailed explanation of the algorithm by Dawkins, the interpretation of the procedure for generating these phrases is open to interpretation. Notice, for example, once the correct letter appears, it stays in place. This led Dembski and Marks [2] to conclude that Dawkins was using a partitioned search. Once a letter is identified, it is locked into place for the remainder of the search. Only one child was used per generation and only those letters not yet correctly identified were mutated.
This interpretation of Dawkins's simulation was, however, wrong. Concerning generations, Dawkins writes [5]
The computer examines the 'progeny' of the original phrases, and chooses the one, however slightly, most resembles the target phrase...
Since "phrases" is plural, Dawkins uses more than one child per generation.
So what was the search algorithm used by Dawkins? Unfortunately, Richard Dawkins no longer has the code he used for the simulation. Copies of the code were apparently distributed to others. Denyse O'Leary, author and blogger extraordinaire, initiated a contest to find the original code [9]. Over 375 responses were received, but no definitive code was identified. There was general consensus that, rather than partitioned search, Dawkins used a Hamming oracle [11].
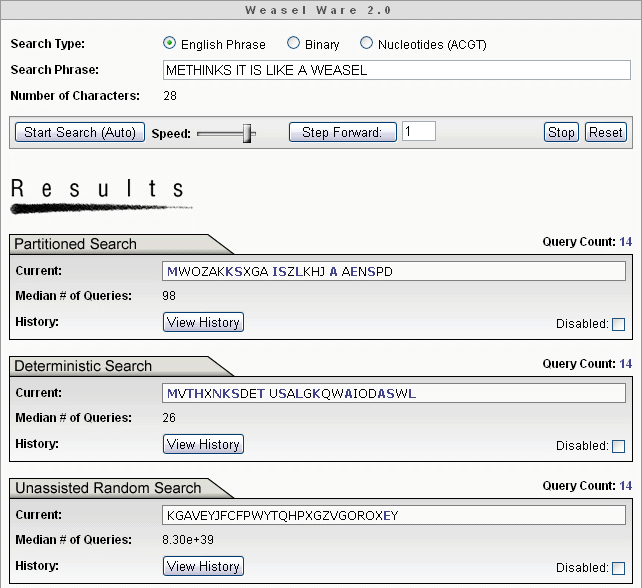
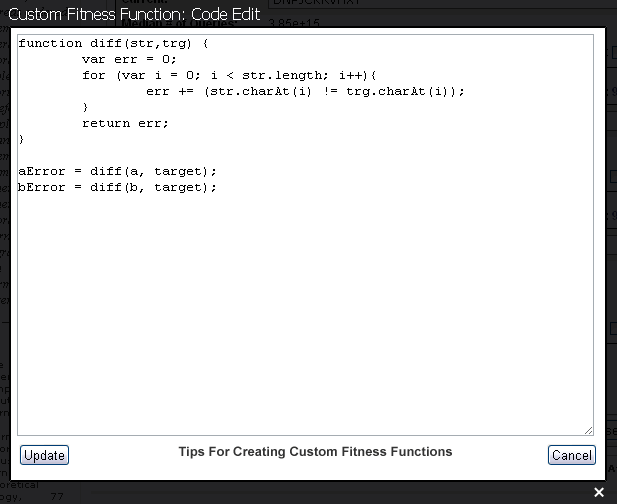
In response, Ewert, Montañez, Dembski and Marks published a paper where various implementations of Hamming oracle solutions to the WEASEL problem are analyzed [11]. They also proposed a deterministic search algorithm, FOOHOA, that outperforms the evolutionary search. You can examine them all with the Weasel Ware Simulation.
The mathematical details for the partitioned search are here [10] and those for the Hamming oracle are here [11].
Ewert et al. [11] also proposed a "search for the search" for the optimal algorithm to extract active information from the Hamming oracle.
The bottom line in all these implementations is the same. The source of the active information in the WEASEL problem is not the evolutionary algorithm. The source of active information is the oracle - either the oracle used in the partitioned search or the Hamming oracle. In fact, the evolutionary search uses the oracle poorly. On a per query basis, active information is seen to be extracted much more efficiently using other means.
Are we sure one of these is the algorithm used by Dawkins? No. But we've covered a lot of bases. If you runs across Dawkins's original code, please let us know.

Oracles
An oracle is a source of active information [3]. Asking an oracle a question is a "query". Oracles, when queried, provide information rich responses.
The game of 20 Questions illustrates the idea of an oracle. The 20 Questions oracle, who has some specific animal, vegetable or mineral in mind, is queried with questions answered with a "yes" or a "no". The search is complete when the object the oracle has in mind is identified.
Answers to queries typically come at a cost. In 20 Questions, each query is valuable in the sense that, after the twentieth question, you have spent all of your queries. In evolutionary computing, answering queries usually uses most of the computing resources. The cost here is thus computer time. The number of queries required for a successful completion to a search is a measure of how much active information is provided by the oracle and how wisely the questioner has used the oracle.
Some oracles are smarter than others. For the WEASEL example, we consider three oracles. The first is a stupid "needle in a haystack" oracle that, when presented with a 28 character string of letters will respond either "no", the character string is not the weasel phrase or "yes", the phrase is the correct answer. If the phrase has only one incorrect letter, the oracle responds with a "no". The oracle provides no indication of whether or not we are close in some sense to the right answer.
A smarter "divide and conquer" oracle, when presented with a string of letters, returns the phrase submitted to it with some of the letters colored red. For example
MPOIUYTRCDDXDSPONHUZARTYUXEL
means "the five letters that are red are correct. The others are wrong." The divide and conquer oracle can provide significantly more active information than a needle in a haystack oracle [6].
The third oracle, a Hamming oracle, is examined below.
An oracle can be used in different ways, some more wisely than others. In the game of 20 Questions, for example, an initial query of "Is it the missing right arm on Michelangelo's statue of David?" will, on average, generate a lot less information that the question "Is it vegetable?" [7].
 Let's imagine a search where letters are first chosen randomly. For each letter, we can envision spinning a roulette wheel and randomly selecting a letter. Once a letter hits at a location, we keep it.
For incorrect letters, we spin the roulette wheel again. We will call this use of the divide and conquer oracle a "partitioned search" [1].
Let's imagine a search where letters are first chosen randomly. For each letter, we can envision spinning a roulette wheel and randomly selecting a letter. Once a letter hits at a location, we keep it.
For incorrect letters, we spin the roulette wheel again. We will call this use of the divide and conquer oracle a "partitioned search" [1].
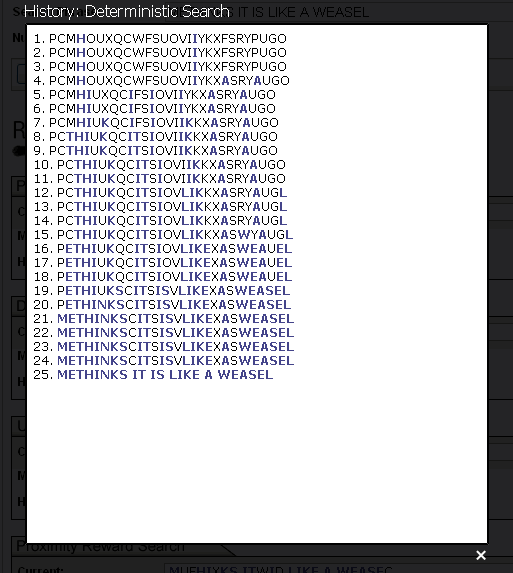
A wiser use of the divide and conquer oracle is "deterministic search." Here, we step through the alphabet one letter at a time. We submit the letter A to the oracle and the oracle tells us all the places in the phrase containing the letter A. Next, we query for the letter B and identify all of the places in the phrase that contain B. Then C, D. ... all the way through Z and the space, * . We are guaranteed to identify the phrase in no more than 27 queries [8].
The deterministic search reveals the enormous information available from the divide and conquer oracle. Using a deterministic search, every letter and space in all of Shakespeare's works can be identified in 27 queries. All of the letters in all of the books in the Library of Congress can be identified in 27 queries! If we wish to distinguish lower from upper case letters, 26 additional queries are required. If we add numbers, punctuation, and other characters to the search, the alphabet increases to some value of N. Independent of the length, L, of the phrase, all of these characters can be identified in at least N queries.

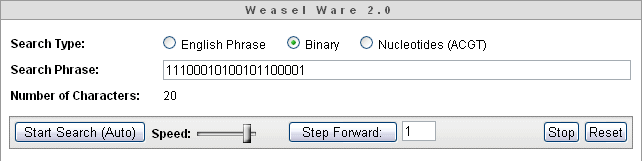
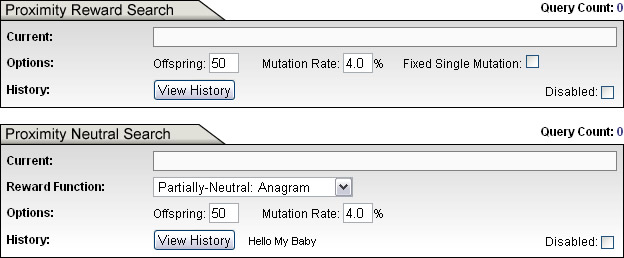
In an Evolutionary Search such as the one proposed by Dr. Dawkins [5], a population of strings, each L letters long, are chosen randomly. Each string is then presented to the Hamming oracle [11] which assigns the string a rank, based on its proximity to a desired target. (Such a ranking function is generally referred to as a fitness function in evolutionary computing.) The string with the closest proximity to the target is selected and chosen as the parent of the next generation of strings, where each child string contains a certain number of mutations. The process is repeated until the target is reached. (In the simulation, we call such an algorithm a "Proximity Reward Search", due to the fact that the rank of each string correlates directly with proximity to target.)
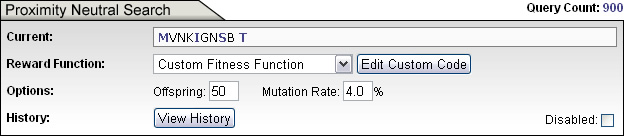
But the rank does not have to do so. For example, we can imagine an Evolutionary Search where rank is based on some internal properties of the strings themselves, such as number of vowels, rather than on external proximity to target. There are many such ways to assign fitness rankings to strings. Some of them are demonstrated in the Simulation GUI and explained in the accompanying documentation for version 2.0. We call these type of searches "Proximity Neutral" searches, since the ranking of strings is done without direct regard to an intentional long-term goal.
As is expected, the perfomance for proximity neutral searching degrades considerably, since we do not provide as much target-specific active information to our search. Simply having replication, mutation, and selection is not enough to ensure convergence on a target; the correct ranking function, specific to a goal target, is also necessary to have a reasonable chance of success. Proximity reward search provides the correct fitness functions needed for the targets (and in doing so provides large amounts of active information), whereas proximity neutral searches typically do not.
We also include "Partially Neutral" searches that do include some target-specific information in chosing ranks for strings, but only applies it in an indirect way. The performance of such searches are better than completely neutral searches, but not as good as proximity reward searches. The improvement in performance is directly proportional to the amount of target-specific active information encoded in and provided by the fitness function.

The probability model for the various searches for
METHINKS*IT*IS*LIKE*A*WEASEL
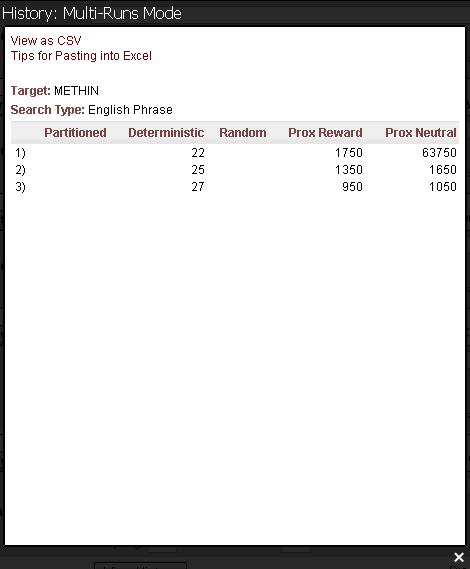
can be modeled using fundamental properties of probability. For those interested, we have a page that covers the math details. For the first three searches, the median number of queries needed to generate a success can be calculated. For the WEASEL phrase, these are as follows.
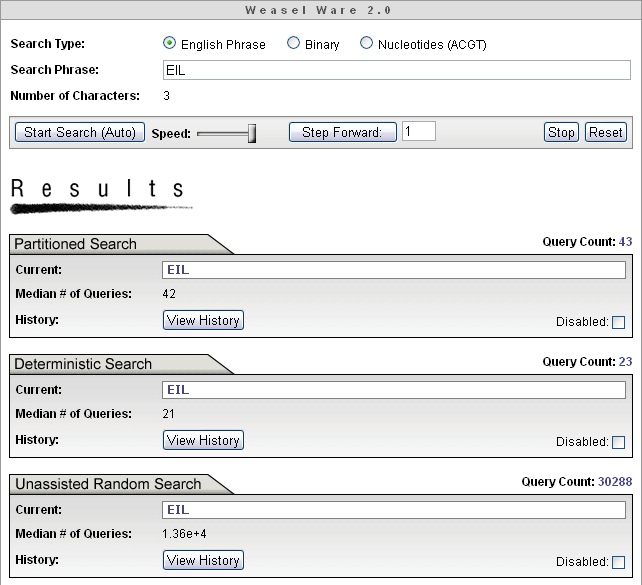
Partitioned search = 98 Queries
Deterministic search = 26 Queries
Random Search = 8.30 x 1039 Queries
= 8,300,000,000,000,000,000,000,000,000,000,000,000,000 Queries
The active information supplied by the "divide and conquer" oracle is necessary to perform the search as is the active information encoded in and extracted from the Hamming oracle in Evolutionary Search.
In evolutionary computing, the active information can be generated by a programmer carefully selecting an appropriate fitness function and skillfully querying an information rich oracle.

References & Footnotes
- [1] William A. Dembski, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence, Rowman & Littlefield Publishers, Inc. (2001).
- [2] William A. Dembski and Robert J. Marks II, "Conservation of Information in Search: Measuring the Cost of Success"
- [3] William A. Dembski and Robert J. Marks II, "Judicious Use of Computational Resources in Evolutionary Search"
- [4] William A. Dembski and Robert J. Marks II, "Horizontal and Vertical No Free Lunch for Active Information in Assisted Searches"
- [5] Richard Dawkins, The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design, W. W. Norton, (1996).
-
[6] Are there even more information rich oracles? Yes. An even smarter oracle, for example, can respond with
MPOIUYTTNJDMDSPONHUOALTDUXELwhere, in addition to the red letters, the pink letters indicate the letter is one letter off from being correct. It is not difficult to concoct even smarter oracles that, when properly used, complete the search in a single query! - [7] Classic information theory says a query made concerning a given set of answers will generate the largest average information when the chances of getting a "yes" is 50-50. See, for example, Thomas M. Cover and Joy A. Thomas, Elements of Information Theory, 2nd Edition, Wiley-Interscience, 2006.
- [8] In the implementation of the deterministic search on the simulation, the search is not done sequentially from A to Z and *. Visualize the characters being printed on 27 cards. The deck is well shuffled and placed face down. The character on the first card is searched first. The character on the second card second, etc. This is the way the deterministic search is performed on the simulation. A fresh shuffle occurs for each implementation.
- [9] Denyse O'Leary, "Uncommon Descent Contest Question 10: Provide the Code for Dawkins’ WEASEL Program." Uncommon Descent, August 26, 2009.
- [10] Winston Ewert, William A. Dembski and R.J. Marks II, "Evolutionary Synthesis of NAND Logic: Dissecting a Digital Organism," Proceedings of the 2009 IEEE International Conference on Systems, Man, and Cybernetics. San Antonio, TX, USA - October 2009, pp. 3047-3053.
- [11] Winston Ewert, George Montañez, William A. Dembski, Robert J. Marks II, "Efficient Per Query Information Extraction from a Hamming Oracle," Proceedings of the the 42nd Meeting of the Southeastern Symposium on System Theory, IEEE, University of Texas at Tyler, March 7-9, 2010, pp.290-297.